题意简述
一棵 $N$ 个节点的树,节点编号 $1 \sim N$,且根节点编号始终为 1。
初始时,节点 $i$ 的颜色为 $c_i$。
$M$ 次操作:
0 u c$\hskip .6em$ 将以 u 为根节点的子树中所有的节点颜色染成 c1 u$\hskip 1.5em$ 输出 u 为根节点的子树中颜色种数
数据范围: $1\leqslant T\leqslant 100$,$1\leqslant N, M\leqslant 10^5$, $1\leqslant c_i\leqslant N$。
题目简析
应该想到要用线段树。
但是如果直接用 DFS 序来表示树中的一段区间的话,维护颜色就举步维艰了。
因为查询是一棵子树的颜色种数,普通的区间标记根本就无能为力。
只好另谋出路。
注意到,在树中,一个节点的颜色只会对其及祖先节点有贡献。
具体地,一个节点的颜色更改可以视作将原来的颜色删除,再添加新的颜色。
这样的话,删除颜色就对该节点及其祖先节点贡献 -1;添加颜色则 +1。
但是,不难发现,有一个问题。
如下图(仅考虑 orange 对祖先节点的贡献):
*** 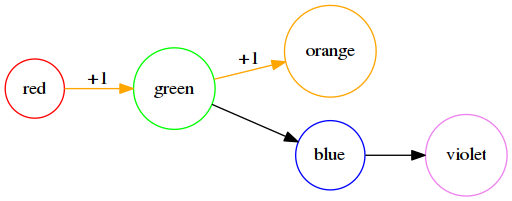 ***
***
上图中,orange 对节点 orange、green 及 red 都有一个贡献值。
但是,如果我们要把 violet 的颜色改成 orange 的话,
则从 violet -> red 这一条链中:
- 删除颜色 所有节点的贡献 -1
- 添加颜色 只对
violet、blue两个节点 +1。
因为,节点red、green已被orange这个颜色更新过了。
如下图(仅考虑将 violet 颜色修改成 orange 对祖先节点的贡献):
*** 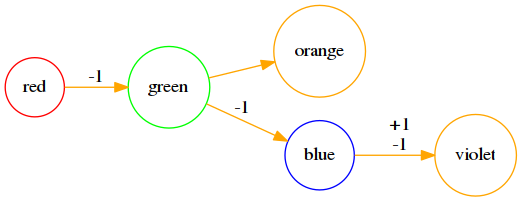 ***
***
不难想到,当修改一个节点 $i$ 的颜色 $c_i$ 时,
我们仅需修改所有与 $c_i$ 颜色相同的节点与 $i$ 的最近公共祖先(所有与 $i$ 构成的最近公共祖先中的距离 $i$ 最近的祖先)
$g(i)$ 到 $i$ 这条路径的所有的节点(包括 $i$,但不包括 $g(i)$ ) 即可。
如何找到 $g(i)$ 呢?
- 假设节点 $i$ 在这棵树先序遍历序列中位置为 $dfs(i)$。
如果节点 $j$、$k$ 颜色和 $i$ 相同,即满足 $c_j=c_k=c_i$; 且对于任意 $dfs(j)\leqslant dfs(i)\leqslant dfs(k)$。
那么,$dfs\big(g(i)\big)=\min \Big\lbrace dfs\big(LCA(i, j)\big), dfs\big(LCA(i, k)\big) \Big\rbrace$。
其中,$LCA(i,j)$ 表示节点 $i$、$j$ 的最近公共祖先。
所以,我们只要对每一种颜色开一棵平衡树,键值为节点的 dfs 序。
然后 lower_bound, upper_bound 一下就可以找到 $j$,$k$ 了。
至于链上的操作树链剖分就可以了。
所以当我们执行一次 操作0 时,要把 $u$ 的子树中所有的颜色删掉,然后仅给 $u$ 添加新的颜色 $c$。
注意到这样一来,一个节点颜色 $c_i$ 就是距它最近的有颜色的祖先(此处,$i$ 视作 $i$ 的祖先)的颜色了。
同时,这样一来,当前节点颜色并没有总是对自己贡献 +1,因为我们始终只考虑了 $u$ -> $g(u)$ 这条路径上的节点;
而 $u$ 的子孙节点其实是有颜色的,且均为 $c$。
所以,查询时如果发现当前节点颜色未在子孙节点中出现,答案 +1。
判断当前节点颜色是否在子孙节点中出现有一个小技巧,详见 *** Code ***。
1 | int flag = 0; |
复杂度分析
由于删除一个节点的复杂度为 $O(\log^2 N)$(树链剖分有一个 $\log$),我们最多添加 $M$ 个节点,
因此时间复杂度为 $O((M+N)log^2N)$。
空间复杂度$O(N)$时间复杂度$O((M+N)log^2 N)$
Hint
据说正解是 $O(N\log N)$ 的,蒟蒻表示不会。
多谢小小兰学长的指教。

