最佳文章

目录
  1. 1. 问题简述
  2. 2. 问题简析
  3. 3. 程序实现

题目链接

问题简述

有 $N$ 个由小写字母构成的单词。
一个串的权值为这个串中每个单词出现的次数的总和（单词可部分重叠）。
求一个长度为 $L$ 串的最大权值。

数据范围：$N$ 个单词长度总和不超过 100，$1\leqslant L\leqslant 10^{15}$。

样例输入：

3 15
agva
agvagva
gvagva

样例输出：

11

问题简析

先将 $N$ 个串建成 Aho-Corasick 自动机，并记 $S$ 为此自动机的状态转移图的节点集。
用 $dp[i][s]$ 表示长度为 $i$ 且最后一个字符在 Aho-Corasick 自动机的节点 s 上的串的最大权值。
显然，答案为 $\max\big\lbrace dp[L][s] \big| s\in S \big\rbrace$。
状态转移：$dp[i+1][s’]=\max\big\lbrace dp[i][s] \big| s\in S \text{且存在从 $s$ 到 $s’$ 的边}\big\rbrace +val[s’]$。
其中，$val[s’]$ 为以该节点结尾的单词的个数（经典的 AC 自动机基础操作，应该懂我在说什么吧。。）

样例的状态图如下

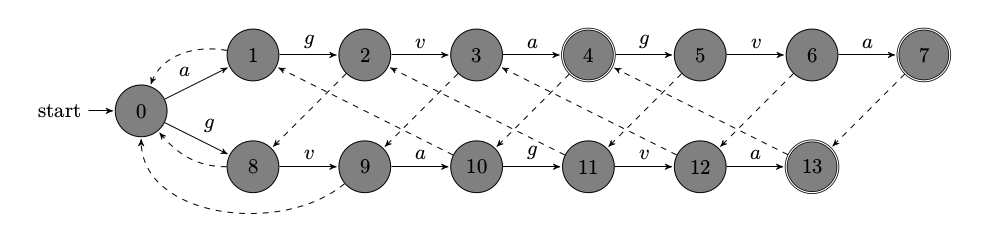
其中，虚线为 fail 指针。
上图中，$val[4]=1, val[7]=3,val[13]=2$，其它节点 $val$ 值为 0。
不难发现，仅考虑有实线的边的转移是最优的；当没有实线的边时，选择虚线的边转移。

接下来就是重头戏了。
我们可以构造一个 $\big|S\big| \times \big|S\big| =14 \times 14$ 的矩阵 $M$
\begin{align}
M[s’][s] = \left\lbrace \begin{aligned}
&val[s’], &\text{存在一条边} s \rightarrow s’ \
&-INF, &\text{不存在一条边} s \rightarrow s’
\end{aligned} \right.
\end{align}
结合前面的状态转移方程有：$dp[i+1][s’]=\max\big\lbrace dp[i][s]+M[s’][s] \big\rbrace$。
可以将 $dp[i]$ 当做一个列向量，那么 $dp[i+1]$ 可以看做由 $M$ 和 $dp[i]$ 进行如转移方程所示的运算规则得到。
对比传统的矩阵乘法，相当于：$\sum$ 变成了 $\max$，同时 $\times$ 变成了 $+$。
不难验证，新的矩阵运算同样是左结合的，这意味着：$dp[L]=M{\color{red}{op}}dp[L-1]=M^{L}{\color{red}{op}}dp[0]$。
接下来，矩阵“快速幂”就好了。

还有一个问题，$dp[0]$ 是什么？
因为零个字符，只能在状态 0，其它状态必须设为负无穷，即：
\begin{align}
dp[0][i] = \left\lbrace \begin{aligned}
&0, &i=0 \
&-INF, &i \neq 0
\end{aligned} \right.
\end{align}
可以通过 $dp[1]=M{\color{red}{op}}dp[0]$ 来验证。

程序实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
#include <queue>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;

typedef long long LL;
const LL  LNF = 0x3f3f3f3f3f3f3f3fLL;

struct Matrix {
    static const int MAXN = 100+10;
    LL M[MAXN][MAXN];
    void fill(LL val) {
        for(int i=0; i < MAXN; ++i)
            for(int j=0; j < MAXN; ++j)
                M[i][j] = val;
    }
    friend Matrix operator * (const Matrix& A, const Matrix& B) {
        Matrix C;
        C.fill(-LNF);
        for(int i=0; i < MAXN; ++i)
            for(int j=0; j < MAXN; ++j)
                for(int k=0; k < MAXN; ++k)
                    C.M[i][j] = max(C.M[i][j], A.M[i][k]+B.M[k][j]);
        return C;
    }
    static Matrix Power(Matrix A, LL X) {
        Matrix ans;
        ans.fill(-LNF);
        for(int i=0; i < MAXN; ++i) ans.M[i][i] = 0;
        for(; X > 0; X>>=1, A=A*A)
            if( X&1 ) ans = ans*A;
        return ans;
    }
    void show(int N=MAXN) const {
        for(int i=0; i < N; ++i) printf("%6d ", i);
        printf("\n------------------------------------------------------------------------------------------------------\n");
        for(int i=0; i < N; ++i) {
            printf("%2d:|", i);
            for(int j=0; j < N; ++j)
                printf("%6d|", M[i][j]);
            printf("\n");
        }
        printf("------------------------------------------------------------------------------------------------------\n");
    }
};

struct AhoCorasick {
    static const int SIGMA_SIZ = 26;
    static const int MAX_NODES = 100+10;
    int ch[MAX_NODES][SIGMA_SIZ];
    int val[MAX_NODES];
    int fail[MAX_NODES];
    int siz;
    
    void Init() {
        siz = 1;
        memset(ch[0], 0, sizeof ch[0]);
    }
    
    int idx(const char c) const {
        return c - 'a';
    }

    void Insert(const char* s) {
        int r = 0;
        for(; *s; ++s) {
            int c = idx(*s);
            if( !ch[r][c] ) {
                memset(ch[siz], 0, sizeof ch[siz]);
                val[siz] = 0;
                ch[r][c] = siz++;
            }
            r = ch[r][c];
        }
        ++val[r];
    }

    void GetFail() {
        static queue<int> Q;
        for(int c=0; c < SIGMA_SIZ; ++c) {
            int o = ch[0][c];
            if( o ) fail[o] = 0, Q.push(o);
        }
        while( !Q.empty() ) {
            int r = Q.front(); Q.pop();
            for(int c=0; c < SIGMA_SIZ; ++c) {
                int o = ch[r][c];
                if( o ) {
                    int fo = fail[r];
                    for(; fo && !ch[fo][c]; fo=fail[fo]);
                    fail[o] = ch[fo][c];
                    val[o] += val[fail[o]];
                    Q.push(o);
                } else {
                    ch[r][c] = ch[fail[r]][c];
                }
            }
        }
    }

    void BuildMatrix(Matrix& mat) {
        mat.fill(-LNF);
        for(int r=0; r < siz; ++r) 
            for(int c=0; c < SIGMA_SIZ; ++c) 
                mat.M[ch[r][c]][r] = val[ch[r][c]];
    }
};

Matrix mat;
AhoCorasick ac;
int N;
LL M;
char s[200];

int main()
{
    ac.Init();
    scanf("%d%lld", &N, &M);
    for(int i=0; i < N; ++i) {
        scanf("%s", s);
        ac.Insert(s);
    }
    ac.GetFail();
    ac.BuildMatrix(mat);
//    for(int i=0; i < ac.siz; ++i) printf("%d, fail[%d]=%d\n", i, i, ac.fail[i]);
//    mat.show(ac.siz);
    mat = Matrix:: Power(mat, M);
    LL ans = 0;
    for(int i=0; i < Matrix:: MAXN; ++i) 
            ans = max(ans, mat.M[i][0]);
    printf("%lld\n", ans);
    return 0;
}